| Name |
Title |
Abstract |
Radu Paltanea |
Inequalities with second order moduli of continuity |
We study some new type of estimates with second order moduli of continuity for positive linar operators and we study the optimality of the constants which appear in these estimates." |
Adrian Branga |
A Class of Parametric Quadrature Formulas with
Higher Degree of Exactness |
In this paper is presented a new class of quadrature formulas depending on two real parameters, which is obtained using Taylor polynomials of even
degree. The value of the second parameter is found out such that the corresponding quadrature formulas have higher degree of exactness. Also we compute the coefficients and using the Peano's Theorem we find a representation of the remainder term. Particularly, the above formula
contains the Simpson, Maclaurin, Newton-Cotes and Gauss-Legendre quadrature formulas.
Keyword: Quadrature formula, Taylor polynomials, Peano's Theorem, Simpson formula, Maclaurin formula, Newton-Cotes formula, Gauss-Legendre formula |
Mircea Ivan |
A Simple Solution to Basel Problem |
The Basel problem is a famous problem in number theory, first posed by Pietro Mengoli in 1644, and solved by Leonhard Euler in 1735.
The Basel problem asks for the precise sum of the series 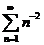
We present a simple proof of Euler's formula  |
Ioan Popa |
A variant of A.Lupas inequality for Peano kernels. |
In this paper we point out a companion of A.Lupas inequality for symmetric kernels and apply it for quadratures. |
Andrei Vernescu |
Some Results in Discrete Asymptotic Analysis |
In this work we present some characterizations by two sided
estimations of the convergence of certain special sequences. |
Bogdan Gavrea
|
Optimization based methods for the simulation of large multi-body
systems. A computational study |
Traditional time-stepping schemes for simulation of multi-body systems are formulated as linear complementarity problems (LCPs) with copositive
matrices. Such LCPs are generally solved by means of Lemke-type algorithms, and solvers such as the PATH solver have proven to be robust. However, for large systems, the PATH solver becomes unpractical from a computational point of view. The convex relaxation introduced by M. Anitescu in 2006 allows the formulation of the integration step as a quadratic program (QP), for which a wide variety of state-of-the-art solvers are available. In the present work we report results obtained when using several well known QP solvers. We investigate computational performance and we adress the correctness of the results from a modelling point of view. |
Gancho Tachev |
New Variants of Voronovskaja-type Theorems for Schoenberg-Spline
Operator |
We represent new quantitative variants of Voronovskaja's Theorem,based on new Estimates for the second moment of Schoenberg Operator.Some conjectures are formulated. |
Ioan Gavrea |
A representation theorem of Lupas type for Hermite-Hadamard Functionals |
In 1974 A.Lupas proved a representation theorem for positive linear fuctionals in terms of divided differences.In this paper we give an extension of this theorem for Hermite-Hadamard functionals. |
Inna Nikolova |
Lowering operators for Multiple Meixner Polynomials of first type |
In this paper lowering operators for multiple Meixner polynomials of first type are found. There are two types of lowering operators for this polynomial set: with fionite difference forward and finite difference backwards. |
Ioana Chiorean |
Remarks on some Parallel Computations for Spline Recurrence Formulas |
It is known that many problems may be solved more accurate by using spline functions instead of finite differences methods. In this way, the computational effort is, also, reduced, even if serial algorithms are used, due to the tridiagonal matrices involved. But this effort can be even more improved by parallel calculus. The purpose of this paper is to give some parallel computation approaches for the recurrence formulas that appear in generating the cubic spline function. |
Marian Olaru |
Data dependence for some functional differential equation in a Banach space |
|
Sorin G. Gal |
Voronovskaja's Theorem and the Exact Degree of Approximation for the Derivatives of Complex Riesz-Zygmund Means |
In this paper we obtain a quantitative Voronovskaja result and
the exact orders in approximation by the derivatives of complex Riesz-Zygmund means in compact disks. |
Ioan Ţincu |
A poof of Schur’s Conjecture and an improvement |
In the paper I proved first Schur's Conjecture by using the properties of Bessel's functions of the first species. The second main result is an identity verified by the product 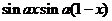 , containing Schur’s Conjecture as a particular case , containing Schur’s Conjecture as a particular case 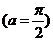 . . |
E.C. Popa |
On an expansion theorem if finite operators calculus of G-C. Rota |
Using so called Viskov method we present here the expansions theorems of the umbral calculus |
Dana Simian, Corina Simian |
ON AN APPLICATION OF IDEAL INTERPOLATION |
Ideal interpolation is obtained when the interpolation conditions, Lambda, have the property that ker(Lambda) is an ideal of polynomials. In case of ideal interpolation we can switch between interpolation and reduction process with respect to a H-basis of the ideal ker(Lambda). It is proved that the interpolation space, for an ideal interpolation scheme, is the same with the space of reduced polynomial modulo a H-basis of the ideal ker(Lambda) and the interpolation operator is the same with the reduction operator. The inner product used in the reduction process is very important Different inner products leads to different reduced spaces of polynomials and therefore to different polynomial interpolation spaces. The aim of this paper is to prove many properties of the polynomials which belong to different polynomial interpolation spaces for ideal interpolation schemes, using the reduction process with respect to a H-basis of the ideal ker(Lambda) and many inner products.. |
Adrian Holhos |
Quantitative estimates for positive linear operators in weighted spaces |
We give some quantitative estimates for positive linear operators in weighted spaces by introducing a new modulus of continuity and then apply these results to the Bernstein-Chlodowsky polynomials.
KEY WORDS: positive linear operators, weighted modulus of continuity, weighted spaces, Bernstein-Chlodowsky polynomials |
Ana Maria Acu, Mugur Acu and Arif Rafiq |
Extremal problems with polynomials |
Using quadrature formulae of the Gauss-Lobatto and Gauss-Radau type, we give some new results for extremal problems with polynomials. Let ~H (®;¯) be the class of real polynomials pn¡1 2Q n¡1, such that
jpn¡1(xi)j · ¯~ P(®+1;¯+1)n¡1 (xi)¯¯¯; i = 1; n where by ~ P(®;¯) n we denote the nth Jacobi polynomial and the xi are the zeroes of ~ P(®;¯)n . We give exact estimation of certain weighted
L2-norms of the kth derivative of polynomials with there are in the
class ~H (®;¯). |
Sofonea Florin |
On a liniear and positive operators |
|
Heiner Gonska |
Quantitative Voronovskaya-type theorems |
At the 2006 NAAT conference in Cluj we presented a new (?) estimate for the Taylor remainder which has many applications in Numerical Analysis and Approximation Theory.
In our talk we will focus on just one group of applications, namely on extensions and generalizations of the classical Voronovskaya theorem for Bernstein operators. As one consequence we obtain several known quantitative Korovkin-type theorems for positive linear operators defined on C[0,1].
More concrete applications will be given for the "genuine Bernstein-Durrmeyer operators" U_n, for a class of operators which bridge the gap between them and the classical Bernstein operators B_n, and for one further class of mappings linking the U_n to the Durrmeyer operators M_n.
Time permitting, we also discuss Voronovskaya-type theorems in terms of the Ditzian-Totik modulus, in simultaneous approximation, and such for the Schoenberg spline operator. |
Eugen Constantinescu |
. |
. |
Eugen Draghici, Daniel Pop, |
Approximation of solution of a polylocal problem using Chebyshev - polynomials
of first and second kind. |
Consider the problem: 
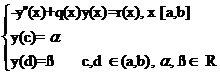
The aim of this paper ist o present an approximate solution of this problem based on Pseudospectral methods. We constract the approximation using Chebyshev collocation methods and use Chebyshev-Gauss-Lobatto interpolation nodes. Using orthopoly polynomials techniques and a Maple implementation, we obtain an analytical expression of the approximation and give examples. |
| Vasile Mihesan |
On A General Class of Beta Approximating Operators |
By using the generalized beta distribution(GB) we obtain general class
of Beta operators,which include both the Beta of the first and
second kind(see [5],[6],[9],[10]).We obtain a several positive
linear operators ,as a special of this Beta operator. |
| Teodora Zapryanova |
A Characterization of K-functional for the Algebraic Version of Trigonometric Jackson Integrals and K-functionals for Cao-Gonska Operators |
We costruct moduli of functions which are a computable characteristic equivalent to the approximation error of algebraic version of trigonometric Jackson Integrals and Cao-Gonska operators. |
| Lucian Beznea |
|
|
| Carmen Violeta Muraru |
|
|
| Dumitru Acu |
A note of Mathieu`s inequality |
In this note we obtain a generalization for Mathieu`s inequality |
| Mioara Boncut |
On Some Properties of Box Spline Functions |
The work has two sections. The first section deals with some box-spline properties related with changing matrix $\Lambda$ in
$a\Lambda$} and the variale $x$ in $x/a, a>0$. The last section
contains the Fourier transform applied to box-spline functions and
some properties of this transformation. |
| Nicolae Secelean |
The continuaity with respect to a parameter of Hutchinson
measure associated of an countable Iterated Functions System with
probabilities |
The continuaity with respect to a parameter of Hutchinson
measure associated of an countable Iterated Functions System with
probabilities |
| Calin Gheorghiu |
|
|

